Easy Tidal Predictions: The Rule Of Twelfths
Although accurately calculating the height of tide between high water and low water will always rely on accurately plotting a tidal curve, there is a way of getting a quick estimate.
We can use the Rule Of Twelfths.
The rule of twelfths provides us with a rough estimate of the height of the tide at hourly intervals between high water and low water.
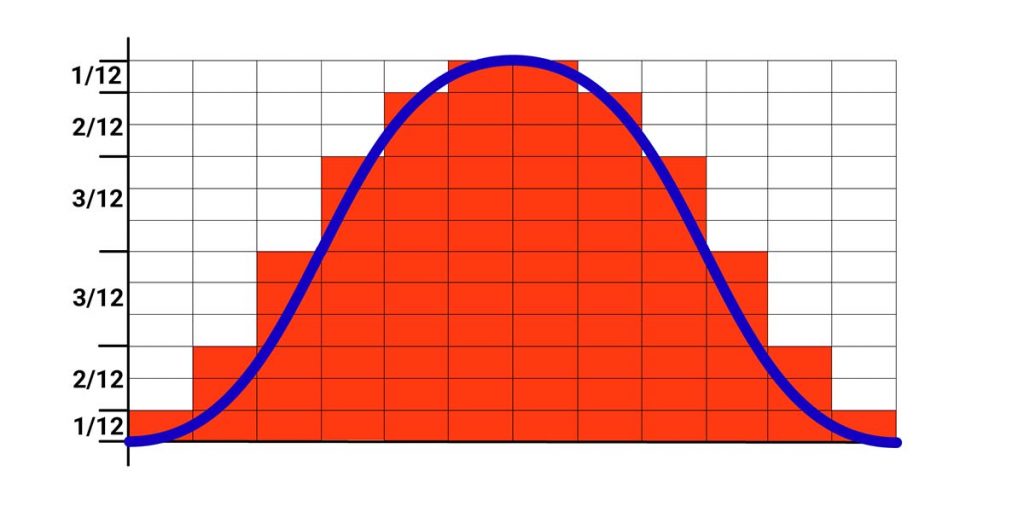
The rule of 12ths assumes that the tide is semidiurnal, approximately following a sine curve with two high waters and two low waters each day.
Around the time of high water and low water, the rate of change of the tide is at its minimum, meaning that you will not notice much of a change at this time.
As the time approaches half tide, however, the rate of change will increase and you’ll notice a large change in the tidal height.
This is reflected in the rule of 12ths, which states that:
during the first hour after low water, the tide will increase by 1/12 of the total range;
during the second hour after low water, the tide will increase by 2/12 of the total range;
during the third hour after low water, the tide will increase by 3/12 of the total range;
during the third hour before high water, the tide will increase by 3/12 of the total range;
during the second hour before high water, the tide will increase by 2/12 of the total range;
during the hour before high water, the tide will increase by 1/12 of the total range.
The Rule Of Twelfths For Tides
The Rule Of Twelfths For Sine Curves
The rule of twelfths is not specifically for tides. It is actually used in mathematics, as an approximation of a sine curve.
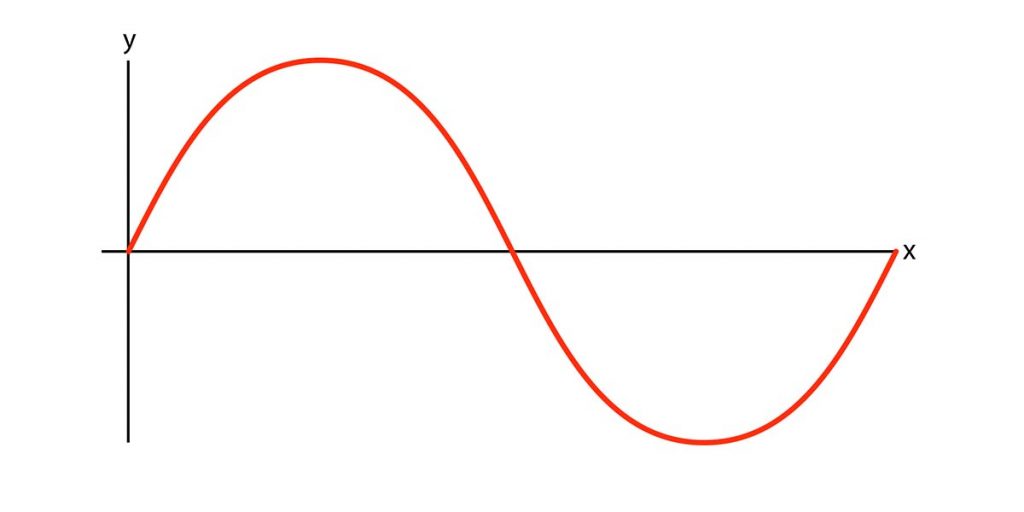
In the image above, you can see a sine curve plotted as y = sin(x).
To approximate the curve, we can use the rule of 12ths instead of needing to use a calculator.
| Step | (x) | Sin (x) | Rule of Twelfths Approximation |
|---|---|---|---|
| 1 | 30° | 0.5 | 0.5 |
| 2 | 60° | 0.87 | 0.83 |
| 3 | 90° | 1 | 1 |
| 4 | 120° | 0.87 | 0.83 |
| 5 | 150° | 0.5 | 0.5 |
| 6 | 180° | 0 | 0 |
| 7 | 210° | -0.5 | -0.5 |
| 8 | 240° | -0.87 | -0.83 |
| 9 | 270° | -1 | -1 |
| 10 | 300° | -0.87 | -0.83 |
| 11 | 330° | -0.5 | -0.5 |
| 12 | 360° | 0 | 0 |
In the case of the sine curve, with the y-axis alternating between 1 and -1, each increment along the y-axis is 0.17.
Similarly, with the x-axis spanning from 0° to 360°, each increment along the x-axis will be 30°.
The rule of twelfths can be used as an approximation of a sine curve, which means that when a tidal curve follows approximately a sine curve, we can similarly use the rule of twelfths for approximating the tide.
Semidiurnal Tides Are Approximately A Sine Curve
Although every tidal curve is unique, semidiurnal tides do generally follow an approximation of a sine curve.
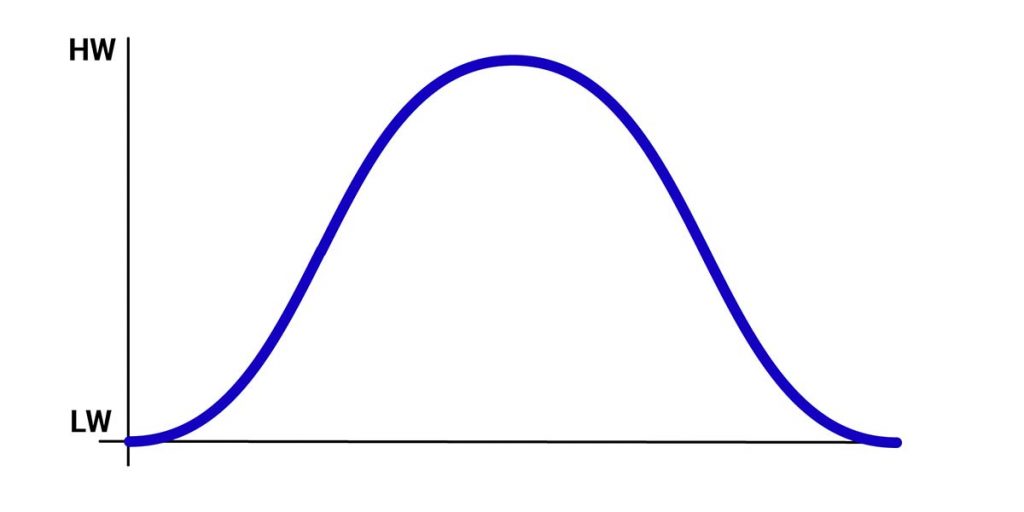
We can look to NOAA for a good explanation of a semidiurnal tide:
An area has a semidiurnal tidal cycle if it experiences two high and two low tides of approximately equal size every lunar day. Many areas on the eastern coast of North America experience these tidal cycles.
NOAA
With two high waters and two low waters each day, we know that there is approximately a 12-hour tidal cycle, corresponding ideally with the rule of twelfths.
This means that we can apply the mathematical rule of twelfths to the specific situation of tidal predictions, using a 1-hour interval.

During the first hour after low water, the tide will rise by approximately 1/12 of the height between low water and high water. During the next hour it will rise by 2/12, then 3/12 and so on.
In the final hour before high water, the rate will slow to approximately 1/12 of the interval again, before turning and beginning to ebb.
Pro Tip: When using the rule of twelfths, remember that it is only an approximation.
The Rule Of Twelfths Is Only An Approximation
When using the rule of twelfths, the key thing to remember is that it is only an approximation.
In mathematics, the rule is only an approximation of a sine curve, and when it comes to tides, a sine curve is only an approximation of a tidal curve.
The Time Between High & Low Water Varies
One of the most obvious illustrations of this approximation is that the interval between successive high or low tides is rarely, if ever, precisely 12 hours.
A more accurate estimate of the interval is actually 12h 20m.
Where we use a 1-hour interval, we should be using a 1h 1.7m interval instead.
Granted, it is not much of a difference, but it does contribute towards the chain or errors than are present.
Tides Do Not Precisely Follow A Sine Curve
While a semidiurnal tide is said to approximate a sine curve, in reality, there are always going to be variations caused by the local geography and other influences.
For example, some areas that look like they would be semidiurnal actually have double-high or double-low waters.
For this reason, you always need to check the area in question to see if the tidal curve looks approximately like a sine curve.
Even if it looks like a sine curve, if you lay a true sine curve over the top you will almost certainly notice some differences.
It may rise quicker and fall slower, or it may linger at high water longer than it lingers at low water.
Pro Tip: Just remember that the rule of twelfths can only ever give you a rough approximation.
Precise Navigation Cannot Use The Rule Of Twelfths
When it comes to sensitive navigation, you cannot use the rule of twelfths to calculate the tide.
As we discussed in the previous section, there are just too many errors that creep in at different steps of the process for it to be used reliably.
The rule of twelfths can, however, be used in circumstances where you just need a guide:
- you want to know when you might be able to row out to your boat;
- you want to know a rough height to go surfing;
- the tidal range is small and you want to go swimming;
- etc.
If, on the other hand, you are navigating a large ship and you need to know what time you will have enough water to get over a sandbank, you’ll need to use actual tidal curves instead.
